Blog - Hyungjin
Biography
I am a Research Scientist, advisory member at EverEx, where I lead the AI research team together with Byung-Hoon Kim. Before joining EverEx, I did my Ph.D. at KAIST where I was advised by Jong Chul Ye. During my Ph.D., I also spent my time as a research intern at NVIDIA Research, Google Research, and Los Alamos National Laboratory (LANL). I pioneered and advanced some of the most widely acknowledged works on diffusion model-based inverse problem solvers. I’m interested broadly in the intersection of generative models, representation learning, and their applications to real-world problems. Here is my CV and Research Statement.
I am looking for highly motivated researchers to work with me at EverEx. If you are interested, send me an email with your CV attached.
- Generative Models (e.g. Diffusion models)
- Inverse Problems
- Mutimodal Representations
- Motion Understanding/Generation
PhD in Bio & Brain Engineering, 2025
KAIST
MS in Bio & Brain Engineering, 2021
KAIST
BS in Biomedical Engineering, 2019
Korea University
Featured Publications
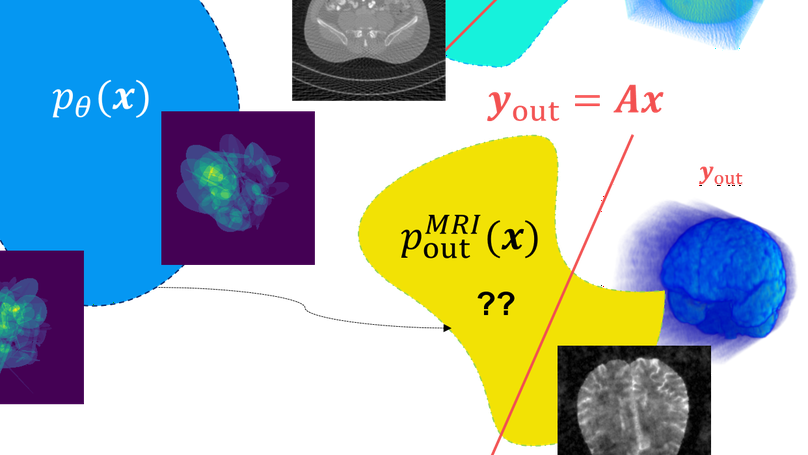
By generalizing DIP, we can design an adaptation algorithm that corrects the PF-ODE trajectory of posterior sampling with diffusion models, such that one can reconstruct from OOD measurements.
Prompt tuning of text embedding leads to better reconstruction quality when solving inverse problems with latent diffusion models.
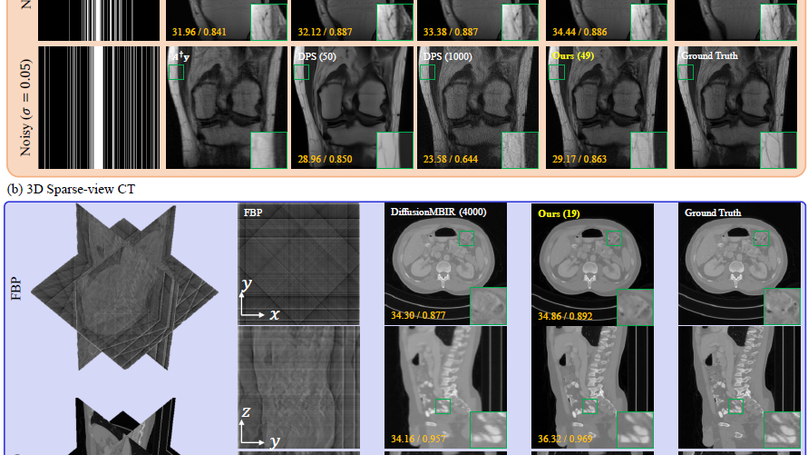
DDS enables fast sampling from the posterior without the need for heavy gradient computation in DIS.
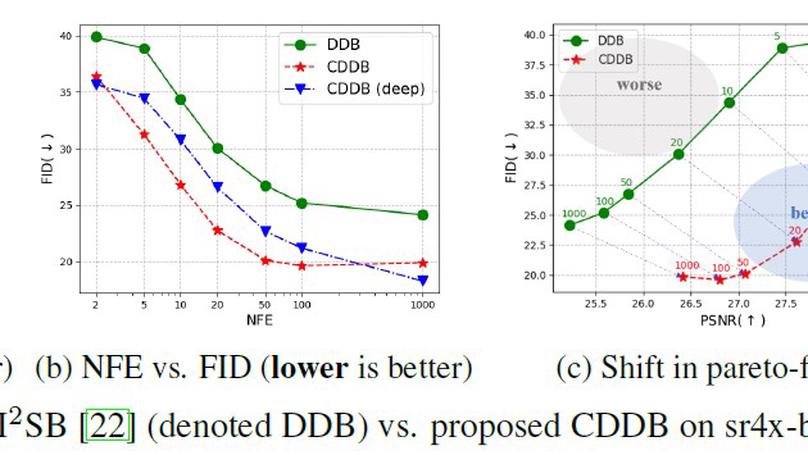
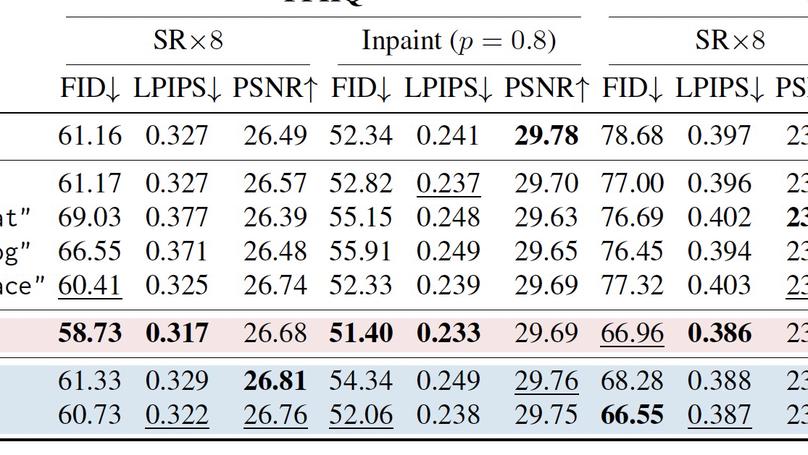
We show that seemingly different direct diffusion bridges are equivalent, and that we can push the pareto frontier of the perception-distortion tradeoff with data consistency gradient guidance.
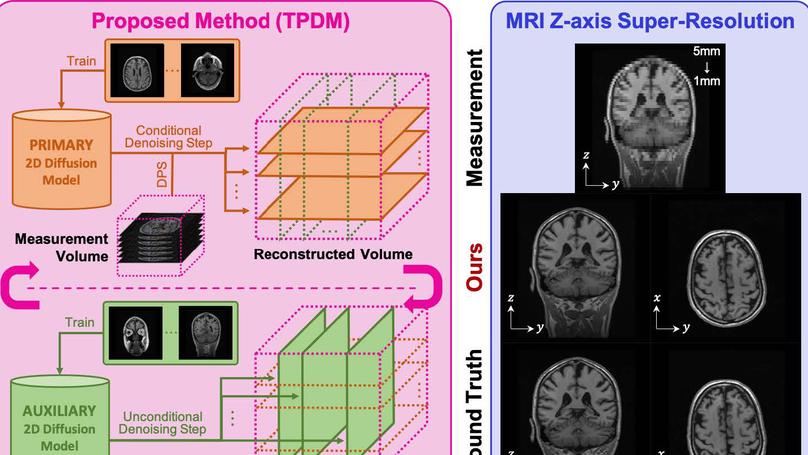
TPDM improves 3D voxel generative modeling with 2D diffusion models. We show that 3D generative prior can be accurately represented as the product of two independent 2D diffusion priors that scale to both unconditional sampling and solving inverse problems.
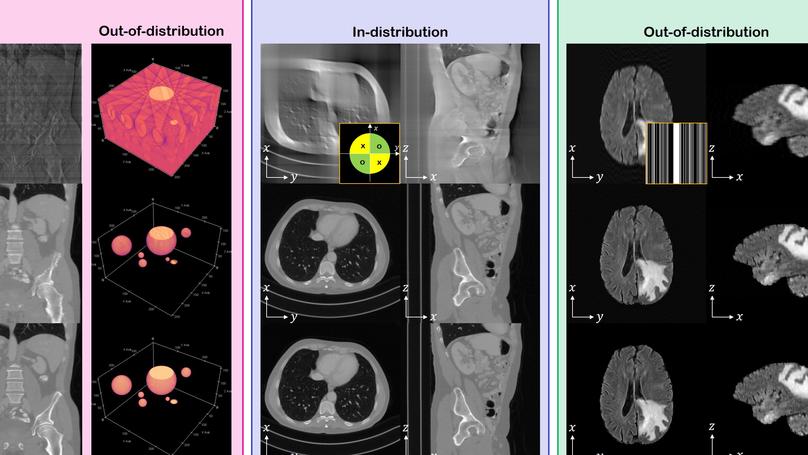
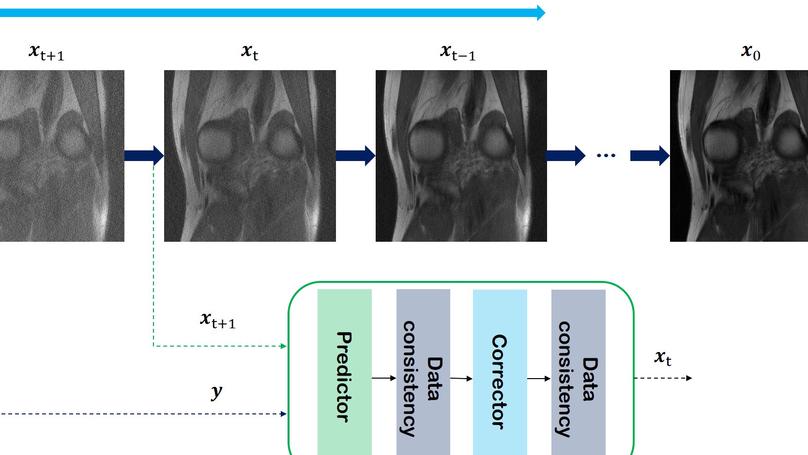
We propose a method that can solve 3D inverse problems in the medical imaging domain using only the pre-trained 2D diffusion model augmented with the conventional model-based prior.

Diffusion posterior sampling enables solving arbitrary noisy (e.g. Gaussian, Poisson) inverse problems that are both linear or non-linear.

Manifold constraint dramatically improves the performance of unsupervised inverse problem solving using diffusion models.

Come-close to diffuse-fast when solving inverse problems with diffusion models. We establish state-of-the-art results with only 20 diffusion steps across various tasks including SR, inpainting, and CS-MRI
Recent Publications
Contact
- hj.chung@kaist.ac.kr
- 291 Yuseong-Gu Daehak-Ro, Daejeon, 34141
- N5-2219
- DM Me
- google scholar
- github